Matemáticas en la esfera del reloj
Hay distintos problemas relacionados con la esfera del reloj, uno puede ser el siguiente:
- A las doce las dos agujas del reloj coinciden en el mismo lugar, a que otra hora vuelven a coincidir.
Efectivamente cuando el reloj indica las 12h tanto la aguja horaria como el minutero están en las 12, el minutero avanza a un ritmo de una vuelta por hora, y la horaria a una vuelta cada 12 horas, a la 1h el minutero completa una revolución e inicia la segunda, alcanzando a la aguja horaria un poco después de la 1h 5m.
-
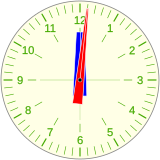
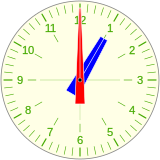

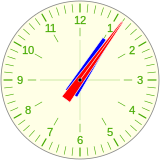
12h 1m 1h 1h 5m 1h 6m
El cálculo de la hora exacta en la que esto sucede da como resultado que en un periodo de 12 horas esta coincidencia se produce 11 veces:
- H_{i}={\frac {12}{11}}\;i}
siendo i un número entero.
La coincidencia inicial se produce para i= 0:
- H_{0}={\frac {12}{11}}\;0=0h}
partiendo de este inicio, la primera coincidencia se produce para i= 1:
- H_{1}={\frac {12}{11}}\;1=1,{\overline {09}}h\;\mapsto \;1h\;5m\;27,{\overline {27}}s}
Si las manecillas continúan girando el minutero adelanta a la aguja horaria y coinciden de nuevo para i= 2:
- H_{2}={\frac {12}{11}}\;2=2,{\overline {18}}h\;\mapsto \;2h\;10m\;54,{\overline {54}}s}
Esta secuencia se repite, resultando que para i= 10:
- H_{10}={\frac {12}{11}}\;10=10,{\overline {90}}h\;\mapsto \;10h\;54m\;32,{\overline {72}}s}
Por último para i= 11, las agujas vuelven a coincidir, dada la aritmética del reloj esta hora es equivalente a la posición inicial con i= 0.
- H_{11}={\frac {12}{11}}\;11=12h\;\leftrightarrow \;0h}





